外資系コンサル就活必須！フェルミ推定の解法解説：実践編

大卒採用試験でも採用される「フェルミ推定」問題の具体的な解き方を解説します。本記事は「基本編」「テクニック編」に続き、就職試験を想定した「実践編」です。実際に就職試験で出された問題や、有名な問題の解き方を解説します。

本記事はコチラの書籍を参考にしています。

就職活動対策シリーズ ― フェルミ推定の教科書

created by Rinker

¥1,100 (2024/11/23 18:29:33時点 Amazon調べ-詳細)

例題１：家庭用電球の年間売上額は？

この問題では、身近な家庭用電球という題材を使っています。身近な題材なので一見すると簡単に解けそうに思えます。

しかし油断すると大変なことになります。簡単そうなのは見かけだけです。

まず「STEP1：前提確認」で「家庭用電球とはなにを指すのか？」をしっかりと定義しましょう。身近な題材がゆえに「前提確認」をスキップしていきなり「STEP２：要素に分解」へ進んでしまいたくなる気持ちを抑えられるかが１つ目の関門です。

「STEP3：細分化」では抜け漏れや矛盾が無いように展開していくと、意外と階層が増えていきます。階層が増えても焦らずに細分化を続けましょう。

それでは、以下に解き方の例の１つを紹介します。
解き方はこれが正解というわけではありませんので、参考の１つにどうぞ。

STEP1：前提確認

「家庭用電球とはどんなものがあるか」を考えてみましょう。

形状別に考えると…
棒形状
丸フラスコのような形状
輪っかの形状
お皿のような形状

大きさで考えると…
手のひらに収まるサイズ
手のひらより大きいサイズ
もっと大きいサイズ

用途で考えると…
居間用の明るいもの
屋外用の防水機能
昼白色に光るもの
暖色に光るもの

と、色々あることに気づきます。これらを別々の要素に分けて考え、後で足し合わせるというのはとても苦労しそうですよね。そこで次のように前提条件を設定しましょう。

前提：形状・材質を問わず明かりを照らすすべての電球が対象とする。

STEP2：要素に分解

さて、次にフェルミ推定の入り口となる基本的な算数の式を作ります。

テクニック編の１．基本方程式にもあるとおり「売上」と来たらこれです。

売上　＝　単価　×　数量

これを使ってこの問題に当てはめます。すると以下のような式が成り立ちます。

家庭用電球の年間売上額　＝　販売単価　×　年間販売数

STEP3：細分化

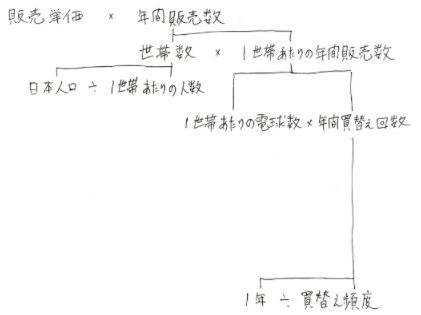
まずは「販売単価」を細分化出来るか考えましょう。細分化の基本は掛け算です。

販売単価　＝　〇〇　×　△△

のように表せるか考えます。うーん、難しそうですね。なので「販売単価」は細分化せずにおきましょう。就職試験でのフェルミ推定問題は時間制限があります。あまり悩んでも仕方が無いので、次のステップに早々に進んでしまうのも戦略です。もし時間が余ったらまたここに戻ってきて解き直せばOKです。

次に「年間販売数」を細分化出来るか考えましょう。上と同じように掛け算の形で考えます。

年間販売数　＝　人口　×　一人あたりの年間販売数
年間販売数　＝　世帯数　×　世帯あたりの年間販売数

などが考えられます。どちらが正解ということはありません。が、この問題では「家庭用」電球の年間販売数を聞かれています。となると「家庭」と同じような単位でまとめるほうが、聞かれていることと解き方に一貫性があり、就職面接では印象が良いです。そこで今回は

年間販売数　＝　世帯数　×　１世帯あたりの年間販売数

を選ぶことにします。

さらに細分化を進めます。次は「世帯数」ですが、これは細分化しようがないのでバスします。

「１世帯あたりの年間販売数」を細分化しましょう。ここで、テクニック編の２．受給一致を活用します。「販売数」を「購入数」と読み替えます。「販売数」と言われるとどのくらいの数字か想像しづらいですが、「購入数」と読み替えることで、自分の身近なことのようになって想像しやすくなります。

１世帯あたりの年間販売数　＝　１世帯あたりの年間購入数

１年間での電球の購入数を考えるには、まず「家庭に電球が何個あるか？」そして「電球はどのくらいの頻度で買い換えるか」を考えましょう。つまり↓の式になります。

１世帯あたりの年間販売数　＝　１世帯あたりの電球数　×　年間買替え回数

最後に「年間買替え回数」は１年を買換え頻度で割れば求められます。この細分化はあっても無くてもどっちでも良いと思います。細かい話なので。

年間買換え回数　＝　１年　÷　買換頻度

STEP4：代入

次に、各項目に数値を代入します。

解説のため、一番上の式の要素にそれぞれA、Bを、それより下段の式に１〜９の番号を振ります。

まずはA：販売単価について、STEP1で家庭用電球を「形状・材質を問わず明かりを照らすすべての電球」と定義しました。なので「販売単価」は、明かりを照らすすべての電球の平均価格となります。電球は安いものは100円ショップで、高いものは国産メーカーのもので数千円します。安い電球は家庭で多く使われますが、高い電球は家庭でせいぜい数個しか使わないでしょう。そうすると、平均して大体500円くらいかな？と考えられます。

次にB：年間販売数について、Bは枝分かれしているので、枝分かれの一番下から代入していきます。

まずは①世帯数の方から攻めてみましょう。③日本人口は皆さんご存知のとおりです。だいたい1.2億人です。日本人口や世界人口はフェルミ推定でよく出る数字です。就活生は暗記しておきましょう。

④１世帯あたりの人数ですが、日本には家族が１０人以上同居する大家族から、一人暮らしまで様々です。近年は少子化、核家族化が進んでいますので、2.5人とします。

すると①は③と④の掛け算で5000万世帯となります。

次に②1世帯あたりの年間販売数の方を攻めます。⑤1世帯あたりの電球数では、家のどこに何個電球があるか想像します。ここでは、図のように場所ごとにいくつ電球があるか数えました。合計で20個となります。

次に⑨買換え頻度です。最近の電球はLEDで寿命が長いです。私の体感で2年に1回くらいかなと思いましたので、2を代入します。

すると、⑥年間買換え回数は⑧と⑨の割り算で0.5となります。更に②は⑤と⑥の掛け算で10個となります。これにより、B：年間販売数は①と②の掛け算で5億個となります。

最後にAとBの掛け算をすると2,500億円となります。

例題２　世界中で現在寝ている人の数は？

この問題は、一見すると規模が大きすぎて混乱してしまいそうになりますが、落ち着いて要素に分解すると、難しい問題では無いことが分かります。

フェルミ推定では、このように一見すると規模が大きくて難しそうに見える「見掛け倒し」問題がいくつかあります。本問題はその良い例だと言えます。

なので就職試験では、このような「見掛け倒し」問題がでたら「ラッキー」と思いましょう。

それでは、以下に解き方の例の１つを紹介します。
解き方はこれが正解というわけではありませんので、参考の１つにどうぞ。

STEP1：前提確認

この問題は、前提確認でほぼ決まります。フェルミ推定の本質からは少しズレますが、この問題のように「前提条件を上手に使うことで、複雑に見えるものごとを見方を変えてなるべく簡単に見えるようにする」という力は、仕事や実生活でもなにかと役立ちます。

鍛えておいて損はしない力なので、就活生だけでなく社会人の方も勉強しましょう。

この問題では、以下のような前提条件を設定します。これは、睡眠時間という一見推測が難しいな情報を、地球の経度(東西方向)という見方から考えるための布石です。

世界の人の1日の睡眠時間は7時間とする。
すべての人は0時〜7時の間で寝る。
人口分布は東西に均一とする。

STEP2：要素に分解

テクニック編の６．母集団の考え方を使います。世界中で寝ている人の数の上限は、世界人口です。世界人口を超える数の人が眠ることはありえません。

世界中で現在寝ている人の数　＝　世界人口　×　睡眠率

STEP3：細分化

実はこの問題では細分化することはありません。ではどうすればいいのか？タネ明かしは次のステップで。

STEP4：代入

ここで、STEP1：前提条件が活きてきます。

睡眠率とは、世界で０時〜７時の間にいる人の割合になります。そしてそれは、世界で０時〜７時の経度にいる人の割合になります。さらに、人口分布は東西に均一なので、経度を２４時間で割ってそのうち７時間が睡眠率になります。

世界人口を72億人、睡眠率は7/24となるので、これを掛け算して答えは21億人となります。

例題３　シカゴにいるピアノ調律師の数は？

この問題は、フェルミ推定では「超」がつくほど有名な問題です。

日本野球界で言うところの長嶋茂雄くらい有名で、フェルミ推定界のレジェンドとも言うべき有名な問題です。

フェルミ推定の書籍を開くと必ず遭遇すると言っても良いくらいの良問なので、就活生はもちろんのこと、社会人の皆様も教養として一度挑戦することをオススメします。

それでは、以下に解き方の例の１つを紹介します。
解き方はこれが正解というわけではありませんので、参考の１つにどうぞ。

STEP1：前提確認

ピアノ調律師という聞き馴染みの無い職業ですが、テンパってはいけません。文字通りピアノに関わる仕事なので、ピアノの数に比例するはずです。

次に、1つ縛り条件を追加しておきましょう。シカゴ外のピアノ調律師がシカゴに出張して仕事をしてしまうと、途方もなく状況が複雑になってしまいます。シカゴ市内のピアノはシカゴ市内のピアノ調律師が調律するという制限をします。

ピアノ調律師の数はピアノの数に比例する。
シカゴ市内のピアノは、全てシカゴにいる調律師が調律する。

STEP2：要素に分解

前提条件で「ピアノ調律師の数はピアノの数に比例する。」としましたので、この考えを逆転させます。すると以下の式が成り立ちます。

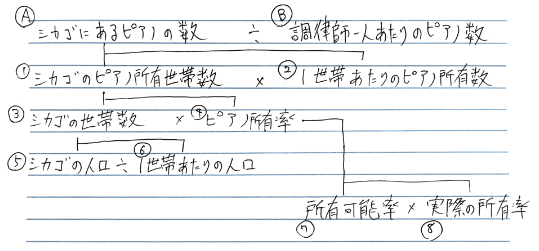
シカゴにいるピアノ調律師の数　＝　シカゴにあるピアノの数　÷　調律師１人あたりのピアノの数

STEP3：細分化（前半）

この問題は細分化が非常に細かくなるので、解説のため細分化を前後半に分けます。

まずは前半「シカゴにあるピアノの数」を細分化していきましょう。ピアノというのは、大きな楽器です。家具の１つと言っても過言では無いほどの大きさです。なので、スマホのように個人で持つというよりは、家族で1台あるかないかというイメージです。そんな時は例題１で使った「世帯」の考え方が便利です。

シカゴにあるピアノの数　＝　シカゴのピアノ所有世帯数　×　１世帯あたりのピアノ所有率

さらに細分化を進めます。掛け算の後半「１世帯あたりのピアノ所有数」は、１台で良いでしょう。家に２つもピアノがあるなんてこと無いですよね？

というわけで掛け算の前半「シカゴのピアノ所有世帯数」の方だけ細分化していきます。ここではテクニック編の６．母集団の考え方がまた活躍します。

シカゴのピアノ所有世帯数　＝　シカゴの世帯数　×　ピアノ所有率

「シカゴの世帯数」は、例題１と同じように、シカゴの人口を１世帯あたりの人数で割ります。

シカゴの世帯数　＝　シカゴの人口　÷　１世帯あたりの人口

次にピアノ所有数は、テクニック編の７．Can-doのテクニックを使います。

ピアノ所有数　＝　所有可能率　×　実際の所有率

STEP3：細分化（後半）

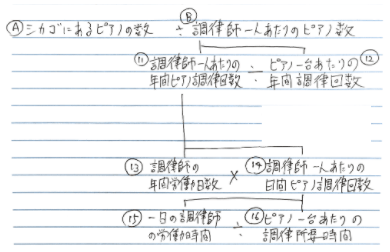
つぎに後半「調律師一人あたりのピアノの数」を細分化してみましょう。

テクニック編の３．時の忘却を使います。例えば「１年間」という期間を決めてこの期間の中で「調律師は何回町調律ができるか」「ピアノは何回調律が必要になるか」という視点で考えてみます。すると以下の式が成り立ちます。ここは慣れが必要な部分です。フェルミ推定の問題をいくつかといてこのテクニックを習得しましょう。

調律師一人当たりのピアノの数　＝　調律師一人あたりの年間ピアノ調律回数　÷　ピアノ１台あたりの年間調律回数

この式の後半「ピアノ１台あたりの年間調律回数」はなんとなく予想できそうな数字ですし、これ以上の細分化は思いつかないので、この部分はこのままにします。

前半の「調律師一人あたりの年間ピアノ調律回数」を細分化しましょう。

年間という言葉に着目します。１年間で何回調律するかは、「労働日数」と「１日に何回調律するか」の掛け算で表すことができます。

調律師一人あたりの年間ピアノ調律回数　＝　調律師の年間労働日数　×　調律師一人あたりの日間ピアノ調律回数

この式の前半「調律師の年間労働日数」は予想できそうですね。前半部分の細分化はやめておきます。後半部分はどうでしょうか。日間という言葉に着目します。１日に何回調律するかは「１日の労働時間」を「１回の調律所要時間」で割ることで求められます。

調律師一人あたりの日間ピアノ調律回数　＝　一日の調律師の労働時間　÷　ピアノ一台あたりの調律所要時間

これで細分化は終了です。

STEP4：代入（前半）

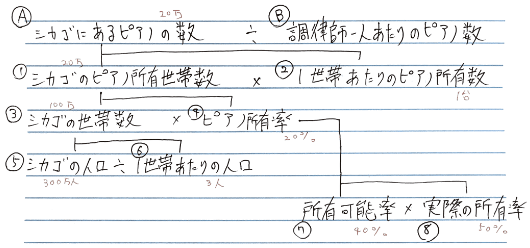
次に代入です。
数が多いので、STEP３のときのように解説のために前後半に分けます。まずは前半「シカゴにあるピアノの数」を求めていきます。

⑦所有可能率について考察します。ピアノは高級品です。ある程度の所得が無いと所有することはできないでしょう。一方でシカゴという土地を想像します。シカゴはアメリカの中でも都市部ですので、住人の所得も他の地域と比べると高い傾向にあることが予想されます。以上から40％という数字を代入します。

次に⑧実際の所有率です。ピアノを所有できるとして、所有するかどうかというところです。みなさんはピアノが所有できるとしたら所有したいですか？日本人の感覚だと「所有したい」という人は10人に1人もいないと思います。その理由の1つに家の中にあっても場所をとっても邪魔という思考がよぎると思います。

一方で、この問題の舞台はアメリカ。家は日本よりもずっと広いでしょう。広い家なら邪魔にならずに気にならないかも。さらにシカゴという所得が高い都市部だということを考えると、私は50％という数字を代入します。

すると、④ピアノ所有率は、⑦と⑧の掛け算になります。0.4×0.5=0.2(20％)となります。

次は⑤シカゴの人口です。シカゴはアメリカの中でも都市部ですが、ニューヨークやワシントンなどの大都市と比べると少ない印象です。海岸沿いの大都市と比べ、内陸に位置するシカゴは冬寒く人口は大都市ほど多くないと想像できます。

とはいっても想像出来ないので、日本のどの都市相当かな？と考えてみます。ニューヨークやワシントンが東京23区だとすると、シカゴはその次の都市なので横浜市くらいでしょうか？横浜市の人口はおよそ300万人なので、⑤には300万という数字を代入します。

次は⑥一世帯あたりの人数です。例題１で日本の一世帯あたりの人数を2.5人としました。アメリカはそれよりは多いイメージがあります。アメリカの映画やドラマを見ると、大学生でも一人暮らしをせずに自宅から通う人が多いイメージです。なので⑥には日本よりチョット多く3人という数字を代入します。

すると③シカゴの世帯数は⑤÷⑥で100万世帯となります。

STEP4：代入（後半）

繰り返しになりますが、代入では一番下の階層から考えていきます。まずは⑮一日の調律師の労働時間です。例えば、朝8時に仕事がスタートして、夕方6時に終わり、そしてお昼に1時間の休憩を挟むとすると、労働時間は9時間になります。

次は⑯ピアノ一台あたりの調律所要時間です。これは完全な憶測ですが、調律というのは簡単な作業ではないでしょう。1時間そこらで終わってしまうような生優しいものでは無いと考えます。一方で、半日も掛かるような作業でもないと思います。というわけで、ここでは3時間と決めます。

すると⑭調律師一人あたりの日間ピアノ調律回数は、⑮9時間÷⑯3時間=3回となります。

次に⑬調律師の年間労働日数を考えます。厚生労働省の発表によると、日本の2018年の年間休日総数の１企業平均は 108.9 日。この数字は、企業において最も多くの労働者に適用される年間休日数を平均したものです。つまり、労働日数は365日-109日=256日。アメリカには感謝祭やクリスマス休暇、サマーバケーションがありますので、もう少し休暇を増やして、切りよく200日とします。

すると⑪調律師一人あたりの年間ピアノ調律回数は、⑬200日×⑭3回で600回となります。

最後に⑫ピアノ一台あたりの年間調律回数です、これは完全に予想ですが、年に1回では少ないような気がします。ピアノは鍵盤をたたくと、鍵盤に繋がったハンマーがピアノ線を叩くことで音が出る仕組みです。つまり音を出す度にピアノ線に負荷が掛かって緩んできます。とはいえワンシーズンに一回も調律するとも思えません。なので間をとって3回とします。

するとB：調律師一人あたりのピアノの数は⑪600回÷⑫3回で200台となります。

最後に、この問題の答えです。A20万÷200=1000人