「フェルミ推定」という言葉を知っていますか?
フェルミ推定とは「実際に調査することが難しいような捉えどころのない量を、いくつかの手掛かりを元に短時間で概算する」考え方です。
本記事はこんな人におすすめ
・就職面接で「フェルミ推定」が出題される就活生
・仕事で困難な問題に直面して頭を抱える社会人
・地頭力、論理的思考力を鍛えたい全ての人類

本記事はコチラ↓の書籍を参考にしています。フェルミ推定についてもっと詳しく知りたい人はコチラよりお求めください。
フェルミ推定は全人類におすすめできる
日本では、コンサルティング企業やIT企業などの就職面接でフェルミ推定を使った問題が出題されますので、これら業界を志望する就活生はフェルミ推定の勉強は必須です。
就活生だけでなく、社会人でも学生でも、フェルミ推定を勉強することで「地頭力」「論理的思考力」を鍛えることができて、学校の成績アップの手助けになったり、会社や家庭のトラブルを効率的に解決する手助けになります。
つまり、フェルミ推定は全人類におすすめできる考え方と言えます。本記事では、フェルミ推定について「基本編」と「実践編」の2回に分けて紹介します。今回は「基本編」です。
フェルミ推定とは?
私(ええぞう)の知る、フェルミ推定を「最も適格で的を得た表現で表した1文」はこちら↓です。
フェルミ推定とは…
「大きすぎて感覚的に予測するのが難しい数値を、要素分解して、知っている情報・感覚的に予想可能な情報の組み合わせにすること」
「大きすぎて感覚的に予測するのが難しい数値」とは?
- 日本全国にあるマンホールの数は?
- シカゴにいるピアノ調律師の数は?
どちらも、フェルミ推定の代表的な問題で、就職面接でも数えきれないほど使われ続けてきた「フェルミ推定と言えばこれだよね」と言えるほどに超有名な問題です。
- 「日本全国」「シカゴ」という広すぎる範囲
- 町中に溢れる「マンホール」という多すぎる量
- 「ピアノ調律師」という多いのか少ないのか分からない量
というところが、「大きすぎて感覚的に予想するのが難しい」理由です。このあたりの数字がぱっと出てくる人は、日本ではクイズ王くらいでしょう。普通の人なら想像することすら不可能です。
しかし、これら「想像すら不可能な数字」を誰でも計算できるようになってしまうのが、フェルミ推定の魅力です。
「要素分解して、知っている情報・感覚的に予想可能な情報の組み合わせにする」とは?
要素分解=数学の因数分解と同じです。
もっと簡単に言うと、四則演算「+」「-」「×」「÷」の組み合わせにすることです。
例えば
日本で1年間に使用されるシャンプーの量は?
という問題があったとしましょう。当然このままでは、予想することは不可能です。
そこで、この問題を
- ①「1世帯が1年で使うシャンプーの量」×②「日本全国の世帯数」
という掛け算に分解してみます。すると、少しだけ想像しやすくなった気がしませんか?
①「1世帯が1年で使うシャンプーの量」はあなたの日々の経験から、何か月に1回シャンプーをドラッグストアで買ってるかを思い出してみましょう。
②「日本全国の世帯数」は、まだ難しいかもしれません。これもさらに分解して
- ③「日本の総人口」÷④「1世帯当たりの人数」
とします。③はだいたい1億2000万人くらいでしょうか?④はあなたの周りの家庭の人数を想像してみて下さい。平均何人くらいでしょうか?
こう考えることで、全く予想不可能だった数字を「知っている情報・感覚的に予想可能な情報の組み合わせ」で計算することができるようになりました。
- 日本で1年間に使用されるシャンプーの量=①「1世帯が1年で使うシャンプーの量」×③「日本の総人口」÷④「1世帯当たりの人数」
フェルミ推定を勉強するメリット
就職活動で使える(就活生向け)
「マッキンゼー・アンド・カンパニー」「ボストン・コンサルティング・グループ」などの外資系コンサル企業の採用試験で多く使われています。他にも「リクルート・ホールディングス」など日系企業でも採用試験に使われているところもあります。
あなたの志望する企業がフェルミ推定の問題を出すかどうかは、今の時代インターネットで検索すればすぐにわかります。もし、あなたの志望する企業や業界がフェルミ推定の問題を出しそうなのであれば、本記事でフェルミ推定を勉強しましょう。
本記事はコチラ↓の書籍を参考にしています。フェルミ推定についてもっと詳しく知りたい人はコチラよりお求めください。
論理的思考力を習得できる(社会人向け)
ビジネスシーンやプライベートで、一見して攻略不可能な問題を要素に分解して解決する力を養うことができます。
例えば
①ムチャなクレーマーへの対応
②達成の難しい四半期営業目標の達成
③製造工程の工数(加工に必要な時間)を半分にする
④どちらも正しい主張をしている身内の喧嘩の仲裁
⑤家計が苦しい時、出費を抑える方法を考える
問題を要素に分解する例
①「会社が悪い点」「お客様の勘違い」に分ける
②「営業マンごと」の細かく現実的な目標に分ける
③「工程1つ1つの所要時間」に分けて一番長い工程を改善
④「お互いの言い分」と「妥協できる点」を整理
⑤「出費」の割合を見て、一番%の大きい費用を節約
上は、あくまでも簡単な例です。実際には周りのいろいろな要因も絡み合っていると思います。しかし、抽象的でふんわりしていてどうやって解決したら良いか分からなかった赤枠が、黄色枠のように分解することで少し問題の中身が具体的で解決出来そうになってきました。
つまり
人生全般における「考える力」が身につくと言えます。
学校の成績アップの手助けになる(学生向け)
学校のテスト問題、特に文章問題ではフェルミ推定と同じように文章を要素に分けることで、問題を解くのがカンタンになります。
例えば(中学数学の問題)
△ABCはBC=12㎝、AC=8㎝、∠BCA=90°の直角三角形である。点Pは頂点Aを出発して毎秒2㎝でCまで進む。同時に点Qは頂点Cを出発して毎秒3㎝でBまで進む。△PCQの面積が9㎝2になるのは出発から何秒後か。
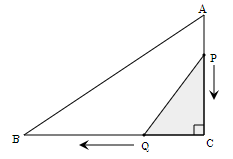
この問題のゴールは「三角形の面積が9㎝2になるのは出発から何秒後か」です。これをⒶ「三角形の面積」とⒷ「何秒後か」という要素に分けてみましょう。
Ⓐ「三角形の面積」は、①「底辺」×②「高さ」÷2 という要素にさらに分けることができます。上の絵を見ると、①「底辺」は「Q~Cの距離」です。②「高さ」は「P~Cの距離」ですね。
Ⓑ「何秒後か」は、求めたい答えなので、「X」を使って表します。
ここで一度、問題文を振り返ってみましょう。
①「底辺」=「Q~Cの距離」について、「点Qは頂点Cを出発して毎秒3㎝でBまで進む」と書いています。
②「高さ」=「P~Cの距離」について、「点Pは頂点Aを出発して毎秒2㎝でCまで進む」と書いています。
①「底辺」=「Q~Cの距離」=3X と言い換えられます
②「高さ」=「P~Cの距離」=8-2X と言い換えられます
この問題のゴールは「三角形の面積が9㎝2になるのは出発から何秒後か」なので、これを式にすると、
9 = 3X × (8-2X) ÷ 2 となります。あとは2次関数の問題を解いていきましょう。
6X2 – 24X + 18 = 0
X2 – 4X + 3 = 0
(X – 1) (X – 3) = 0
X = 1 , 3
答え:1秒後と3秒後
フェルミ推定のやり方
例題
日本で1年間に使用されるシャンプーの量は?
Step1.問題を要素に分解
フェルミ推定の大原則は要素への分解です。まずは、例題を2つの要素の掛け算に分解します。
- ①「1世帯が1年で使うシャンプーの量」×②「日本全国の世帯数」
Step2.要素をさらに分解
①をさらに分解します。
- ①「1世帯が1年で使うシャンプーの量」=Ⓐ「シャンプー1本の容量」×Ⓑ「1世帯が1年で使うシャンプーの本数」
②もさらに分解します。
- ②「日本全国の世帯数」=Ⓒ「日本の総人口」÷Ⓓ「1世帯当たりの人数」
例題「日本で1年間に使用されるシャンプーの量は?」を、以下のように分解することができました。
- Ⓐ「シャンプー1本の容量」×Ⓑ「1世帯が1年で使うシャンプーの本数」×Ⓒ「日本の総人口」÷Ⓓ「1世帯当たりの人数」
Step3.要素に数字を代入
Ⓐ 大きいものは1リットルくらいあるなぁ。小さいのは200mlくらいかな?平均すると400mlくらいかな?
Ⓑ 自分の経験上3か月に1回くらい買い替えてる気がする。12か月÷3か月=4本くらいかな?
Ⓒ 確か1億2000万人くらいだっけ?
Ⓓ 大家族も一人暮らしもいるよなぁ。最近は核家族化が進んでいるから2.5人にしよう
- Ⓐ400ml×Ⓑ4本×Ⓒ1億2000万人÷Ⓓ2.5人=76,800,000,000ml=76,800,000リットル
上の例は、あくまでも1例です。フェルミ推定に正解はありません。
- 「1回の洗髪でプッシュする回数」×「1プッシュで出るシャンプーの容量」×「1人が1日に洗髪する回数」×「365日」×「日本の総人口」
のように他のアプローチから分解することもできます。
就職試験で時間が短い場合はこれでも十分ですが、時間があればもっと細かい要素に分解することができます。就職試験で時間に余裕があれば可能な限り細かくしましょう。社会人であれば、細かくするほど問題を解決するためのアプローチのバリエーションが増えて、より効果的な対策を講じることができます。
まとめ
フェルミ推定とは…
「大きすぎて感覚的に予測するのが難しい数値を、要素分解して、知っている情報・感覚的に予想可能な情報の組み合わせにすること」
日本では、コンサルティング企業やIT企業などの就職面接でフェルミ推定を使った問題が出題されますので、これら業界を志望する就活生はフェルミ推定の勉強は必須です。
就活生だけでなく、社会人でも学生でも、フェルミ推定を勉強することで「地頭力」「論理的思考力」を鍛えることができて、学校の成績アップの手助けになったり、会社や家庭のトラブルを効率的に解決する手助けになります。
つまり、フェルミ推定は全人類におすすめできる考え方と言えます。本記事では、フェルミ推定について「基本編」と「実践編」の2回に分けて紹介します。今回は「基本編」です。
本記事はコチラ↓の書籍を参考にしています。フェルミ推定についてもっと詳しく知りたい人はコチラよりお求めください。
フェルミ推定のトリビア
「フェルミ推定」の名前の由来は物理学者でノーベル物理学賞を受賞したエンリコ・フェルミに由来します。フェルミはこの種の概算を得意としていました。
正確な計算ではなく、おおよその値を計算する「概算」の達人であったといわれ、原子爆弾の爆発の際、ティッシュペーパーを落とし、その動きから爆風を計算し、爆発のエネルギーを見積もったという逸話があります。
参考サイト・関連記事
参考サイト↓
Wikipedia:エンリコ・フェルミ
Wikipedia:フェルミ推定
中学校数学学習サイト
関連記事↓
外資系コンサル就活必須!フェルミ推定の解法解説:実践編 (eezoublog.com)
フェルミ推定の基本テクニック10選!地頭力(論理的思考力)を鍛えよう! (eezoublog.com)



