フェルミ推定の基本テクニック10選！地頭力(論理的思考力)を鍛えよう！

フェルミ推定とは「実際に調査することが難しいような捉えどころのない量を、いくつかの手掛かりを元に短時間で概算する」考え方です。

日本では、コンサルティング企業やIT企業などの就職面接でフェルミ推定を使った問題が出題されますので、就活生は必須です。

就活生だけでなく社会人・学生でも、フェルミ推定を勉強することで「地頭力」「論理的思考力」を鍛えることができて、学校の成績アップの手助けや、会社や家庭のトラブルを効率的に解決する手助けになります。

特に就職面接でのフェルミ推定では、抑えるべきテクニックがあります。そのテクニックを10個紹介します。

本記事はこんな人におすすめ
・就職面接で「フェルミ推定」が出題される就活生
・仕事で困難な問題に直面して頭を抱える社会人
・地頭力、論理的思考力を鍛えたい全ての人類

本記事はコチラ↓の書籍を参考にしています。フェルミ推定についてもっと詳しく知りたい人はコチラよりお求めください。

就職活動対策シリーズ ― フェルミ推定の教科書

created by Rinker

¥1,100 (2024/11/23 18:29:33時点 Amazon調べ-詳細)

基本方程式
受給交換
時の忘却
キャパシティ
回転率
母集団
Can-do
プロセス
セグメンテーション
はさみうち
まとめ
フェルミ推定のトリビア
参考サイト・関連記事

基本方程式

１．売上＝単価×数量
　　（単価…販売単価、客単価、拠点数）
　　（数量…販売数、客数、拠点あたりの売上）
２．利益＝売上ー費用
３．利益＝売上×利益率

この３つの方程式は、就職面接におけるフェルミ推定の基礎中の基礎となります。就活生はぜひ丸暗記しましょう。

社会人にとっては、この３つの方程式が基本であることは重々ご存知だと思います。しかし、目の前の業務や日々の忙しさに目を奪われてしまうとついつい頭から抜け落ちてしまう恐れもあります。今一度復習しましょう。

受給交換

受給交換の方程式
生産量＝販売量＝購入量＝使用量

「需要と供給は一致する」という原則（仮定）です。

問題
「ティッシュペーパーの年間生産数は？」

と聞かれると「そんなのティッシュペーパーのメーカーの人じゃないからわからないよ」と諦めてしまいそうになります。

そこで、これを「ティッシュペーパーの年間使用量は？」と言い換えると、自分の生活ベースから想像しやすくなります。

現実世界では、作った分だけ売れるわけではありません。作ってから購入されて使用されるまでにタイムラグがあります。なので、言葉遊び感を覚えるかもしれません。

しかし、このテクニックを覚えることで「目線を変える力」「問題の難易度を下げる力」が身につきます。就活生のみならず、社会人にも習得してもらいたいテクニックです。

時の忘却

これはテクニックというよりは「注意事項」です。フェルミ推定の問題を解くことに集中しすぎるあまり「時」「時間軸」を忘れてしまうから注意しようね、という意味です。

問題
「日本における育毛剤の売上は？」

と聞かれた時に、「売上」＝「ある一定期間における販売数と単価の掛け算」となることを忘れないように注意しましょう。問題文に「１年間における」と期間が明記されていれば忘れないですが、わざと書いていない場合もありますので、就活生はよくよく注意しましょう。

就職面接でフェルミ推定を解く場合は、まずこの期間を前提条件として、面接官に質問もしくは宣言する必要があります。

上の例において、前提条件として「期間は１年」とし、さらに「需供一致」テクニックと組み合わせることで、この問題文を「１年間における日本での、育毛剤の使用量と販売単価を掛けた合計金額はいくらか？」と言い換えることができます。

「時の忘却」テクニックは就活生だけの問題ではありません。社会人でも、時を忘却してしまう人は少なくありません。以下の例を読んでドキッとした人は、フェルミ推定を勉強して「時を忘却しない」癖を身に着けましょう。「時は金なり」とも言います。時は有限で貴重なリソースです。時を忘却することは、あなたの貴重な資源を、自ら無駄遣いするようなものです。

社会人が時を忘却する例
お客さんとつい話し込んでしまい、次回訪問予定を確認し忘れた。
上司の指示をメモるばかりで、その仕事の納期を聞き忘れた。

キャパシティ

キャパシティは日本語で「容量」を意味する英語です。フェルミ推定においては「ものごとには上限がある場合があるから注意しましょう」ということを意味します。数値に限界がある問題の場合、以下の方程式を使うことができます。

キャパシティの方程式
上限　×　割合
席数　×　稼働率（搭乗率）

問題
ハワイ行きの飛行機の１本あたりの乗客数を求めよ

という問題の場合、次のように式を作ると大きく間違えてしまう場合があります。どこが間違っているか分かりますか？

１本あたりの乗客数　＝　行きたい人の数　×　実際に行く人の数　÷　便数

この式は一見正しいように見えます。しかし、飛行機１便あたりの席数に限界があることが考慮されていません。日本人の半分がハワイに行きたいと思って、そのうちの1/3が実際にハワイに行って、１日１０便の飛行機が飛んでいる場合、

１本辺りの乗客数　＝（１億2000万人÷2）÷　３　÷　10　＝　200万人

となってしまいます。200万人乗れる飛行機なんて現実存在しません。SFの宇宙戦艦でもそんなには乗れません。

ちなみに、上の計算式では「時の忘却」テクニックもやらかしています。このように、フェルミ推定では、基本テクニックをしっかり抑えておかないと、トンデモナイ非現実的な計算になってしまいます。十分注意しましょう。

「キャパシティ」を考慮して、以下のように考えます。

1本辺りの乗客数＝席数×稼働率

座席は、例えば日本〜ハワイ直行便なら、小さい飛行機は使いません。200人〜300人くらい乗れるジャンボジェット機を使うこともあるでしょう。おおよその席数は予想できそうになってきました。

稼働率は、繁忙期や閑散期によって変わりそうですが、航空会社もそんなことは分かっています。繁忙期は便数を増やして、閑散期は減らします。航空会社としては、赤字にならないような稼働率が欲しいわけです。もし飛行機で海外に行ったことがある人なら、体感で稼働率は分かるのでは無いでしょうか？座席が半分近く空いているということはまず無いですよね？稼働率は結構高いと予想できます。

こう考えると、1便200万人より、ずっと現実的な計算ができそうです。

回転率

「キャパシティ」テクニックに似た考えです。回転率とは「同じ人やモノが一定期間において何回カウントされるか」を意味します。

例えば、ラーメン店の1日の来客数を考える場合、席数に限りがあるので「キャパシティ」テクニックを見逃してはいけません。それに加えて、お客さんがラーメン店で食事をする時間は短いので、同じ席に何度もお客さんが座ります。これが「回転率」です。

問題
自動車の年間販売数は？

このとき、次のような式を立ててしまうと、間違った計算になってしまいます。どこが間違っているか分かりますか？

自動車の年間販売数　＝　世帯数　×　1世帯あたりの自動車台数

このように計算してしまうと、各世帯で毎年自動車を買い換えることになってしまいます。しかし実際には車の買い替え頻度は低いので、次のように計算し直しましょう。

自動車の年間販売数　＝　世帯数　×　1世帯あたりの自動車台数　×　年間購入回数

「×年間購入回数」は「÷買い替え頻度（年）」と言い換えてもOKです。ちなみに、この問題で「需供一致」を使って「自動車の年間販売数＝自動車の年間購入数」と言い換えると、買い替え頻度を忘れにくくなるかもしれません。

母集団

「キャパシティ」テクニックと似たテクニックです。「キャパシティ」テクニックは席数のような目で見て限界が分かる場合に使いますが、母集団は”あえて”限界を設けるテクニックです。

問題
メガネを掛けている日本人の数は？

という問題の場合、日本の総人口を母集団として使います。すると

メガネを掛けている日本人の数　＝　日本の総人口　×　メガネを掛けている人の割合

という式になります。「日本の総人口」は想像付きますし、「メガネを掛けている人の割合は」あなたの周りの人を10人程度思い浮かべてみれば、ざっくりの割合はすぐに出てきます。

Can-do

「母集団」テクニックを更に発展させたテクニックです。「母集団」テクニックだけでは、まだ精度は低いので、より高い精度を求める場合に、本テクニックを利用しましょう。当然、就職面接でライバル達に差をつけるためには、より精度の高い（考察の深い）計算ができたほうが良いですので、特に就活生には身につけてほしいテクニックです。

「母集団」テクニックでは、「母集団×割合」で計算しましたが、「割合＝可能な割合×実現する割合」と更に分解します。

Can：可能な割合　−　Do：実現する割合　という意味です。

問題
日本人のジェット機の利用人数を求めよ

という問題の場合、「母集団」テクニックだけを使うと以下の式となります。このままでは「利用率」の部分がフワッとしています。

ジェット機の利用人数＝母集団（日本の人口）×利用率

そこで、「Can-do」テクニックを使って「利用率」をさらに分解しましょう。

ジェット機の利用人数＝母集団×利用可能率（Can）×実際に利用する率（Do）

さっきよりはいくらか分かりやすくなってきました。飛行機代は高額なのである程度の収入が無いと利用することは難しいでしょう。このことから「利用可能率」を計算出来そうです。収入があっても実際に利用するかどうかはまた別問題です。あなたやあなたの周りの人が、どれくらいの頻度でジェット機を使っているか想像してみましょう。

しかし、これでもまだ少しフワッとしています。そこで、上で説明した「時の忘却」テクニックや、後ほど説明する「セグメーション」テクニックを使うことでさらに細かく分解して、知っている・想像しやすい数字にすることができます。

プロセス

「Can-do」テクニックと本質的には一緒です。「Can-do」テクニックは人口などの”数”を使って絞り込む方法ですが、「プロセス」テクニックは、人の行動やモノの流れのような”時間軸”を使って絞り込む方法です。

仕事で、製造工程の改善（加工時間を短くしたり、不要な工程を取り除く）をしたり、煩雑な事務手続きを簡素化する時に「プロセス」テクニックの考え方を使うと、現状の問題点が発見しやすくなり非常に便利です。マーケティング分析にも良く使われる方法なので、社会人はぜひ習得しましょう。

問題
コンビニにおけるタバコの購入者数は？

という問題のときに、購入者がタバコを買うまでの過程（プロセス）で分解してみましょう。すると以下の式が成り立ちます。

購入者数　＝　コンビニ入店者数　×　レジに行く割合　×　レジでタバコを注文する割合

この時「例外が無いこと」を必ず確認しましょう。つまり「コンビニでタバコを買うためには、必ずコンビニに入店して、必ずレジに行って、必ずレジでタバコを注文しなければ買えない」という文章が成り立つかどうかを確認しましょう。

この方法以外でコンビニでタバコを購入できてしまう場合、この式では不十分で例外が存在することになります。例外の場合での購入者数も別で計算しなくてはいけません。

逆に、就職面接では「レジで注文するタイプのコンビニに限る」「コンビニ店外に自販機がある場合は除く」のように前提条件を設定することで、問題をシンプルにして対策ができます。

セグメンテーション

このテクニックは汎用性が高く、使用頻度も高いです。思考の幅が広がり、網羅性が高まり、抜け漏れやダブリを予防することができるので、就職面接でライバル達に差をつけたいなら、何度も練習して習得しましょう。

同じ理由で、社会人にも有用なテクニックです。MECE（漏れ無くだぶり無く）思考が自然と身につき、作業のやり直しや後戻りが激減して、仕事がスムーズに進み、仕事の成果が上がって、ストレスが減ります。

「セグメーション」テクニックとは、母集団をいくつかのセグメント（区切り）に分解するテクニックです。簡単に言うと表を作ることです。

問題
日本のゴルフ人口は何人？

という問題の場合、「母集団」テクニックを使って以下の式を作ります。

日本のゴルフ人口　＝　日本の総人口　×　ゴルフ人口率

この時「ゴルフ人口率」はイメージしづらいです。なぜイメージしづらいのでしょうか？例えば「女性より男性に人気」「若い人より成人に多い」というように、複雑な感じがするからパッとイメージできないのです。

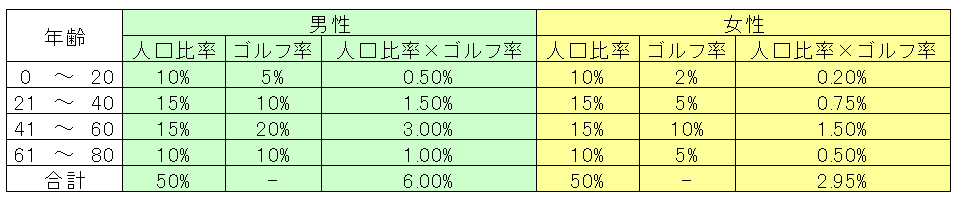
そこで「性別」「年齢」で表を作ってみましょう。男女比は１：１とします。年齢別人口分布は、0〜20歳：20%、21〜40歳：30%、41〜60歳：30%、61〜80歳：20%　とします。ゴルフ人口率は「女性より男性のほうが多い」「41〜60歳が一番多そう」というイメージで考えます。すると、以下のような表が書けます。

「人口比率×ゴルフ率」の男女の合計値から、6.00% + 2.95% = 8.95%が「ゴルフ人口率」として算出できます。

はさみうち

本テクニックは「キャパシティ」テクニックに似たテクニックですが、フェルミ推定の本質からは少し外れた推定方法のため、使いすぎないことをオススメします。就職面接で考える時間が短すぎる場合などにのみ使いましょう。

「キャパシティ」テクニックでは、席数などの上限を設けました。「はさみうち」テクニックは、似たようなもので上限や下限を求めるテクニックです。

問題
コンタクトレンズの利用者数は？

という問題の場合、「メガネだけを使う人はいる」「メガネもコンタクトも使う人はいる」「メガネは使わず、コンタクトだけ使う人は聞いたこと無いなぁ」と考えて、「コンタクトレンズの利用者数はメガネ利用者数よりは少ない」と上限を決めることができます。

社会人であれば、すぐに回答しなければならない時に、エイヤーで答える時に便利ですが、相手に推定方法を問われるとツッコミどころ満載で、あなたの評価を落としてしまう可能性もあります。使い方は注意しましょう。「エイヤーで計算すると〇〇くらいです。エイヤーなので席に戻って計算し直してから正式に回答します」と答えておくのがスマートかと思います。