NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「集合問題」を解説します。学習する際には、適切な問題集を使いこなすことが重要です。NMAT・JMATの集合問題に対する対策は、初級から上級まで段階を踏んで取り組むことがポイントです。この記事では、問題の難易度や対策方法について解説します。NMAT・JMATの集合問題をマスターしましょう。
結論:集合問題でオススメの解き方
- 単純な2~3グループに分ける問題ならベン図が便利
- 複数問が関連するときは、ベン図は不向き。直交表を使う
NMAT・JMATをもっと勉強したい↓
NMAT・JMATとは?
NMAT
NMAT(エヌマット)は、管理職の適性を相対的に測定できる適性検査です。結果は標準得点(偏差値)で表示され、役職タイプ別の適性と指向も評価されます。基礎能力や性格特徴を測定し、キャリア開発に活用できます。
NMAT(エヌマット)公式サイト│リクルートMSの適性検査 (recruit.co.jp)
JMAT
JMAT(ジェーマット)は「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。
試験の内容
NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。
- 検査Ⅰ:言語能力適正検査(国語) 約30分
- 検査Ⅱ:非言語能力適正検査(数学) 約40分
- 検査Ⅲ:性格検査
- 検査Ⅳ:指向検査 Ⅲ,Ⅳ合わせて40分
この中でも「検査Ⅱ:非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。
NMAT・JMATは難しい?
NMATやJMATの難易度は人によって異なります。特に国語や数学の部分は、就職活動でWebテストを受験したことがある人にとっては経験があるものですが、そうでない人にとっては普段から使うスキルではないので、NMAT/JMATのために勉強が必要です。
集合問題を始めとする各種問題に習熟すれば、解く際のスムーズさも増します。定期的な練習が重要です。
NMAT/JMATおすすめ問題集
NMATやJMATの問題解決を支援するため、様々な問題集が存在します。これらの問題集を用いて、問題解決能力の向上を図ることが肝要です。
「集合」初級のテスト出題・練習問題
集合初級の問題では、基本的な概念や集合演算などが出題されることが一般的です。問題を解く際には、例題や公式を活用することが重要です。
例題
30人のクラスでアンケートを取った。電車が好きと回答したのは10人。自動車が好きと回答したのは15人。電車も飛行機も好きだと回答したのは5人のとき、電車も飛行機も好きでないと回答した人は何人か?
この例題では、「電車が好き」「自動車が好き」のアンケートをしているので、「電車」か「自動車」の単純に2グループに分けることができます。
このように単純に2つのグループに分けることができるときは「ベン図」を使うと簡単に解けます。
ベン図とは、四角の中に、2つの円があり、2つの円の一部が重なり合った図です。中学校の数学で学んだのを覚えている人も多いのではないでしょうか?
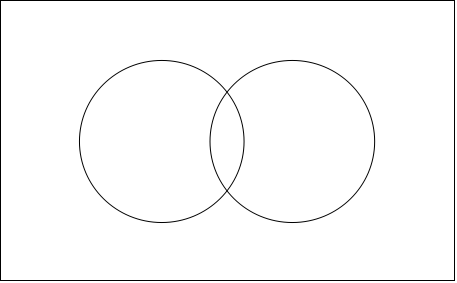
では、ベン図を使ってこの例題を解いていきましょう。ベン図では四角の枠を全体の数とします。この例題では「クラスの人数の30人」が当てはまります。
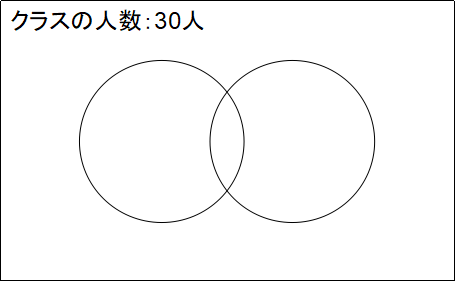
続いて、四角の中の円には登場するグループに含まれる数が入ります。この例題では「電車が好き」「自動車が好き」と回答した人の数が当てはまります。
例えば、左の円を電車が好きと回答した10人、右の円を自動車が好きと回答した15人とします。
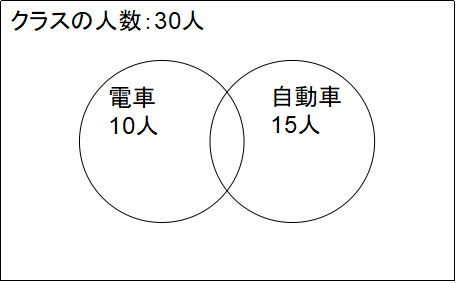
続いて、2つの円の重なり合った部分は、両方の円のグループに属する数が入ります。この例題では「電車も自動車も好き」と回答した5人です。
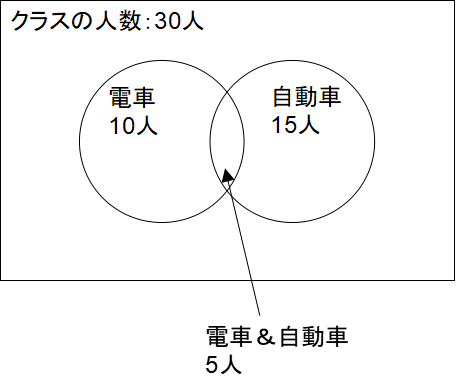
そして最後に、四角の中ですが円の外のエリアには、円に含まれない数が含まれます。この例題では、問題として問われている「電車も自動車も好きではない」と回答した人の数が入ります。
さて、ではこの「四角の中だが円の外のエリア=電車も自動車も好きではない人数」をどうやって求めれば良いのでしょうか?答えは
- 四角の中だが円の外のエリア = 四角の面積 – 2つの円の面積
で計算すると求めることが出来ます。

四角の面積は、クラス30人ということが既に問題文から判明しているので良いですが、2つの円の面積をどうやって求めれば良いのでしょうか?答えは
- 2つの円の面積 = 左の円の面積 + 右の円の面積 – 重なり合った部分の面積
で計算すると求めることができます。左右の円の面積を足すと、重なり合った部分の面積が2重に計算されてしまうことになります。なので、重なり合った部分の面積を1回引いてあげることで、2つの円の面積を求めることができます。

すると、以下のように答えを求めることができます。
電車も自動車も好きではない人数 = 四角の面積(30人) – (2つの円の面積(左の円の面積(10人) + 右の円の面積(15人) – 重なり合った部分の面積(5人)) = 30 – ( 10+15 – 5 ) = 10人
答え:10人
この計算方法は良く出題される方法ですので、必ず覚えておきましょう。AでもBでも無い=全体 – (A+B-(AとBの重なった部分))をしっかり理解しておきましょう。この例題の他には
- 犬も猫も好きでない人=全員 – (犬が好きな人+猫が好きな人-両方好きな人)
- コーヒーも紅茶も飲んだ人=全員-(コーヒーを飲んだ人+紅茶を飲んだ人-両方飲んだ人)
- 電車でもバスでの通勤しない人=全員-(電車通勤の人+バス通勤の人-両方使って通勤する人)
などがあります。
「集合」中級のテスト出題・練習問題
集合中級の問題では、初級よりも複雑な集合の概念が問われます。例題を解くことで複雑な問題にも対応できるようになります。
例題
男女100人に街頭アンケートを行いました。アンケートは、犬・猫飼っていますか?という内容でアンケートの結果は以下のようになりました。
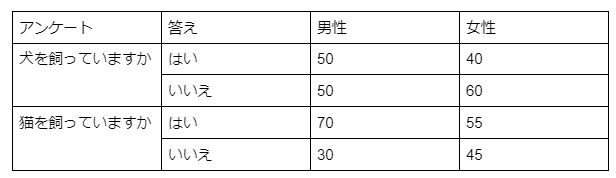
男性で、犬は飼っているが猫は飼っていないと答えた人は20人でした。
- 問1:男性で犬か猫どちらかを飼っている人は何人でしょう?
- 問2:女性で犬も猫も飼っていると答えた人は10人いました。では女性で犬も猫も飼っていない人は何人いるでしょう?
- 問3:猫は飼っていないが犬は飼っていると答えた人は男女合わせて何人でしょう?
初級の問題は、クラス30人に対して2つの質問をアンケートしたので、ベン図を1つだけ描けば解くことができましたが、今度は男女100人ずつにアンケートをしています。
この場合男女それぞれでベン図を描いてみましょう。なお、ベン図に記入する人数は各質問に「はい」と答えた人数とします。
例題の表の下に男性で犬のみ飼っている人の人数が記されています。そこでベン図の描き方に工夫が必要になってきます。「犬を飼っている」数を円の外側に、「犬のみ飼っている」を円の内側に書くことで、区別しやすくしておきましょう。このテクニックは非常に重要です。ここを書き間違えてしまうと、問題文を勘違いして理解することになり、不正解になってしまうため必ずこのテクニックを習得しましょう。
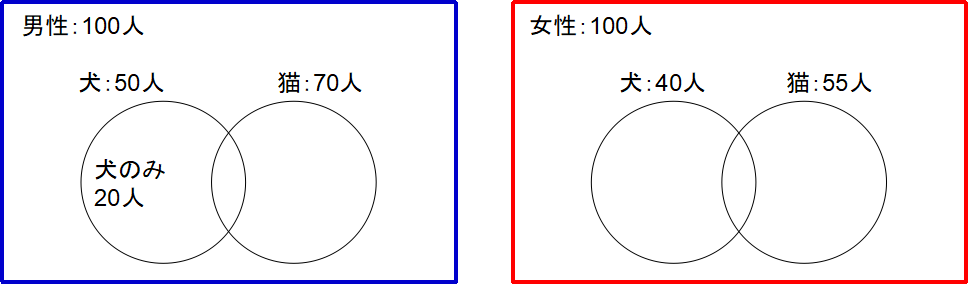
問1:男性で犬か猫どちらかを飼っている人は何人でしょう?
「男性で」とあるので男性のベン図に注目します。「犬か猫どちらかを飼っている人」とは言い換えると「犬のみ飼っている人」+「猫のみ飼っている人」ということになります。
この考え方は、良く出るので覚えておきましょう。この他にも
- 電車か自動車どちらか好きな人=電車のみ好きな人+自動車のみ好きな人
- コーヒーか紅茶どちらかを飲んだ人=コーヒーのみ飲んだ人+紅茶のみ飲んだ人
- 電車かバスどちらかで通勤する人=電車のみ通勤の人+バスのみ通勤の人
が例として挙げられます。
さて例題に戻ります。「犬のみ飼っている人」は問題文のとおり20人です。すると、犬を飼っている50人-犬のみ飼っている20人で、2つの円の重なり合った部分(犬も猫も飼っている人)が30人と求められます。
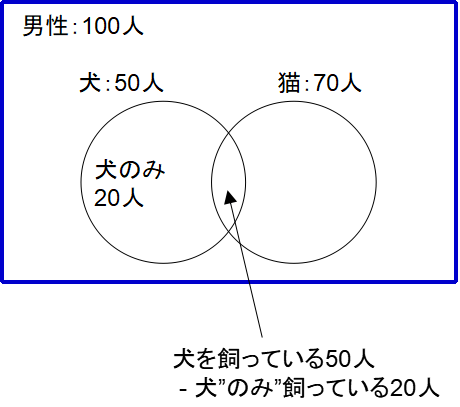
すると、さらに猫を飼っている70人-2つの円の重なり合った部分(犬も猫も飼っている人)30人で、猫のみ飼っている人が40人と求められます。
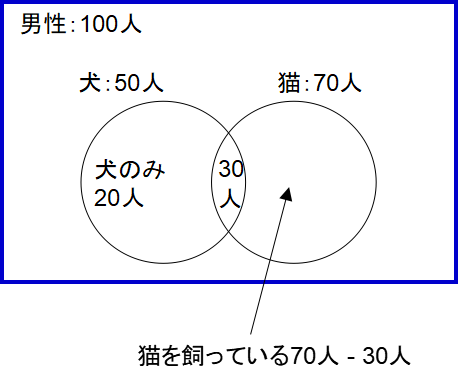
問題で問われている「男性で犬か猫どちらかを飼っている人」は「男性で犬のみ飼っている20人」+「男性で猫のみ飼っている40人」になります。
答えは、60人です。
問2:女性で犬も猫も飼っていると答えた人は10人いました。では女性で犬も猫も飼っていない人は何人いるでしょう?
次の問題は女性について問われているので女性のベン図に注目します。「女性で犬も猫も飼っていると答えた人は10人」とは、2つの円の重なり合った部分が10人ということになります。
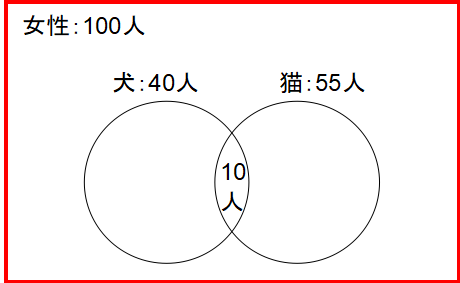
この後は、初級と同じ解き方をします。犬も猫も飼っていない人=全員100人-(犬を飼っている人に40人+猫を飼っている人55人-犬も猫も飼っている人10人)です。


答え:15人
問3:猫は飼っていないが犬は飼っていると答えた人は男女合わせて何人でしょう?
今度は、男女両方が質問されていますので、男女両方のベン図に注目します。「猫は飼っていないが犬は飼っている」とは言い換えると「犬のみ飼っている人」となります。
つまり「男性で犬のみ飼っている人」+「女性で犬のみ飼っている人」を求めれば良いということになります。今まで書き加えてきたベン図を使って計算します。
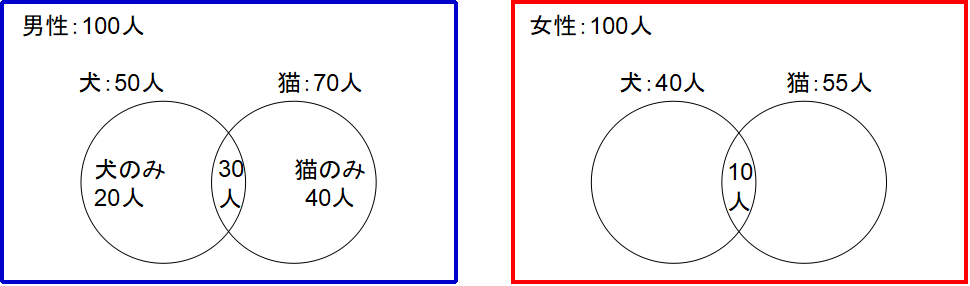
「男性で犬のみ飼っている人」は問題文で20人と分かっています。「女性で犬のみ飼っている人」は、女性で犬を飼っている人40人-女性で犬も猫も飼っている人10人で、30人となります。
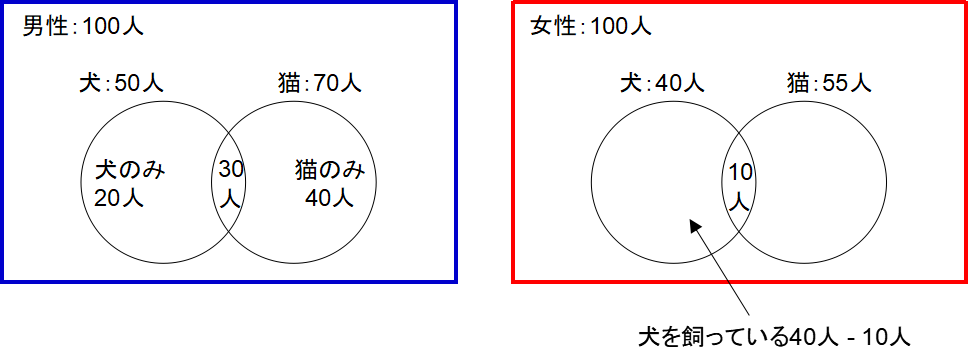
「男性で犬のみ飼っている人」が20人、「女性で犬のみ飼っている人」が30人。
答え:50人
「集合」上級のテスト出題・練習問題
集合上級の問題は、より高度な集合理論や応用問題が出題されます。継続的な練習と理解を重ねることで、高得点を目指しましょう。
例題
イベントに参加した男女50人にアンケートをした結果以下の通りになった。

- 問1.男性で関東に住んでいる人が20人だったとき、女性で関西に住んでいるのは何人でしょう?
- 問2.関東に住んでいる会社員が関西に住んでいる会社員の3倍だったとき、関西に住んでいる自営業者は何人でしょう?
- 問3.男性の会社員が30人、関東に住む女性の自営業者が5人のとき関西に住む女性の自営業者は何人でしょう?
今までの例題では「電車か自動車か」の2択、「男か女か」「犬か猫か」の2×2択のみでしたのでベン図を使って解くことができました。
しかしこの問題のように「男か女か」「関東か関西か」「会社員か自営業化」と3×2択となると、ベン図を使って解くことは不可能ではありませんが、時間が掛かってしまいます。時間制限が厳しいJMAT・NMATでは致命的です。この時は直交表を作れば素早く解くことができます。
問1.男性で関東に住んでいる人が20人だったとき、女性で関西に住んでいるのは何人でしょう?
この問題では「性別」と「住所」が登場してきますので、この2つで直交表を作ります。直交表とは、下のような表です。縦と横にそれぞれ性別と住所を割り当てます。
さらに右端、下端には合計の人数を記入する枠も設けておきます。
| 関東 | 関西 | 合計 | |
| 男性 | |||
| 女性 | |||
| 合計 |
問題文の表を見てみましょう。男性は35人、女性は15人の合計50人です。これをこの表に当てはめていきます。右端の男性の合計を35人、女性の合計を15人。次に問題文の表を見てみましょう。
関東に住む人は30人、関西に住む人は20人です。下端の関東の合計に30人、関西の合計に20人を当てはめます。一番右下はそれぞれの合計人数になります。このアンケートは合計50人にされているので50人が入ります。
| 関東 | 関西 | 合計 | |
| 男性 | 35 | ||
| 女性 | 15 | ||
| 合計 | 30 | 20 | 50 |
問1の「男性で関東に住んでいる人が20人」とありますので、「男性」と「関東」が交わるマスに20人と入れます。
20人と記入したマスの行(横)を見てみましょう。合計35人で関東に20人入っていますので、関西は35-20=15人になります。次に20人と記入したマスの列(縦)を見ていきましょう。
| 関東 | 関西 | 合計 | |
| 男性 | 20 | 35 | |
| 女性 | 15 | ||
| 合計 | 30 | 20 | 50 |
合計30人で男性が20人入っていますので女性は30-20=10人になります。
| 関東 | 関西 | 合計 | |
| 男性 | 20 | 15 | 35 |
| 女性 | 10 | 15 | |
| 合計 | 30 | 20 | 50 |
問題文で問われている「女性で関西に住んでいる人」は「女性」と「関西」が交わるマスを埋めれば求めることができます。
行(横)方向で計算すると15-10=5人。列(縦)方向で計算すると20-15=5人。
| 関東 | 関西 | 合計 | |
| 男性 | 20 | 15 | 35 |
| 女性 | 10 | 5 | 15 |
| 合計 | 30 | 20 | 50 |
答え:5人
問2.関東に住んでいる会社員が関西に住んでいる会社員の3倍だったとき、関西に住んでいる自営業者は何人でしょう?
この問題文では「住所」と「職業」が登場しますので、この2つを使って直交表を作成します。問題文にて「関東に住んでいる会社員が関西に住んでいる会社員の3倍」とありますので、関西に住む会社員をX人とすると関東に住む会社員は3X人となります。
さらに問題文の表から直交表の埋められるところを埋めていくと、以下の直交表を作ることができます。
| 関東 | 関西 | 合計 | |
| 会社員 | 3X | X | 40 |
| 自営業 | 10 | ||
| 合計 | 30 | 20 | 50 |
上の表の会社員の行(横)を見てみましょう。3X人とX人を足して40人となります。これを式にして解いていきます。
- 3X + X = 40
- 4X = 40
- X = 10人
すると、上の表は次のように変化します。
| 関東 | 関西 | 合計 | |
| 会社員 | 40 | ||
| 自営業 | 10 | ||
| 合計 | 30 | 20 | 50 |
次に関東と関西の列(縦)の空白の欄を埋めていきます。
| 関東 | 関西 | 合計 | |
| 会社員 | 40 | ||
| 自営業 | 0 | 10 | 10 |
| 合計 | 30 | 20 | 50 |
答え:「関西に住んでいる自営業者」は10人
問3.男性の会社員が30人、関東に住む女性の自営業者が5人のとき関西に住む女性の自営業者は何人でしょう?
最終問題は複雑です。問題文に「性別」「住所」「職業」の3つが出てしまいました。しかしうろたえる必要はありません。落ち着いて順番に解いていきましょう。
問題文の一番はじめに「男性の会社員」というヒントが出ていますので「性別」「職業」で直交表を作ってみましょう。下のような直交表が出来上がります。
| 男性 | 女性 | 合計 | |
| 会社員 | 30 | 40 | |
| 自営業 | 10 | ||
| 合計 | 35 | 15 | 50 |
次に空欄を埋めていきます。埋めた結果がこちらです。
| 男性 | 女性 | 合計 | |
| 会社員 | 30 | 10 | 40 |
| 自営業 | 5 | 5 | 10 |
| 合計 | 35 | 15 | 50 |
次にもう一度問題文を振り返ってみます。「関東に住む女性の自営業者が5人」というヒントがあります。上の表を見ると、女性で自営業者なのは5人となりました。さらに問題文から「関東に住む女性の自営業者が5人」ということが分かっています。
- 女性の自営業者5人 = 関東の女性の自営業者5人 + 関西の女性の自営業者?人
という式が成り立ちます。
答え:0人
まとめ
NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「集合問題」を解説します。
結論:集合問題でオススメの解き方
- 単純な2~3グループに分ける問題ならベン図が便利
- 複数問が関連するときは、ベン図は不向き。直交表を使う
NMAT・JMATをもっと勉強したい↓




