NMAT・JMATとは、大学入試センターが実施する適性検査および問題集です。SPI(大学入試センター試験)に代表される言語能力テストや適性検査により、性格や公式能力を客観的に測定し、適性についての情報を提供します。NMATやJMATには、例題やアドバイザーによる解説が豊富にあり、言語能力や適性検査の準備に役立ちます。
結論:割合問題でオススメの解き方
- 割合の問題は「比べられる量/元の量=割合」基本
- 複雑な問題文でも、文脈を1つ1つ整理する
- 割合の問題では、すぐに具体的な金額の計算をしない
- 「残りの」という表現に気をつける
NMAT・JMATをもっと勉強したい↓
NMAT・JMATとは?
NMATは「管理者適正検査」と呼ばれ、中間管理職への昇進試験で使われる検査方法です。JMATは「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。
- 検査Ⅰ:言語能力適正検査(国語) 約30分
- 検査Ⅱ:非言語能力適正検査(数学) 約40分
- 検査Ⅲ:性格検査
- 検査Ⅳ:指向検査 Ⅲ,Ⅳ合わせて40分
この中でも「検査Ⅱ:非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。
NMAT割合 初級の例題_短い文章
下の例題には「割合」の問題を解くのに必要な基本的な考え方が詰まっています。下の例題をすべて解けますでしょうか?試してみましょう。
例題
1.〇人の40%は550人である。
2.ある本の60%を読み終えたところ50ページ残った。この本は何ページあるか?
3.ある部活のメンバーが今年は20%増えて210人になった。昨年は何人だったか?
解説1
例題1
〇人の40%は550人である。
割合の問題(パーセントや分数)が出てきたらまず頭に思い浮かべてほしい数式があります。それがこちら↓
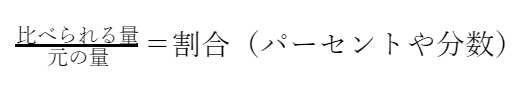
問題文に出てくる「比べられる量」を分子に、「元の量」を分母にすると、イコール割合になります。
この問題では
- 比べられる量=550人
- 元の量=〇人
- 割合=40%=40/100
となります。これを数式に当てはめてみましょう。
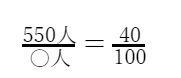
分数の計算式を解くときは、=の左右の両方の分母を、掛け算します。
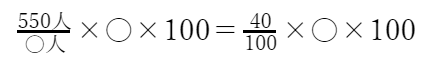
すると、=の左側では分母の〇が消えて、=の右側では分母の100が消えます。
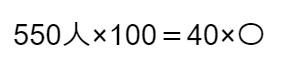
〇の数字を求めるために、=の左右を40で割ります。

すると答えはこうなります。
答え:〇=1375人
解説2
例題2
ある本の60%を読み終えたところ50ページ残った。この本は何ページあるか?
この問題でも、1問目で使った↓の式を使います。
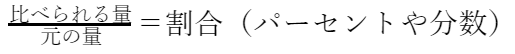
この式に問題文を当てはめてみましょう。すると下のような式が完成します。

この式では「読み終えたページ数」と「本の総ページ数」の両方が分からない数字なので、これでは式を解くことができません。ここで大事になってくるのが言い換えの考え方です。「読み終えたページ」を別の言い方で言い換えてみましょう。それがコチラ↓
- 読み終えたページ = 全ページ – 残ったページ
これを元の式に当てはめるとこうなります。
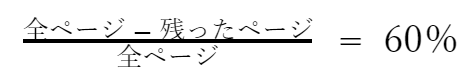
60%を別で表現すると 0.6となります。さらに、上の式を約分します。
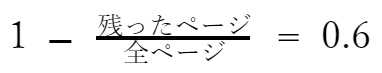
残ったページ数は50ページなので
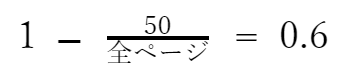
両辺に全ページを掛け算します。
- 全ページ – 50 = 0.6*全ページ
- 全ページ – 0.6*全ページ = 50
- 0.4*全ページ = 50
- 全ページ = 50÷0.4 = 125
答え:125ページ
別解2
例題2
ある本の60%を読み終えたところ50ページ残った。この本は何ページあるか?
この問題を解く方法がもう一つあります。それは問題文を読みかえてしまう方法です。
「60%読み終えた」ということは、残ったページ数は全ページの40%になります。100%-60%=40%だからです。
つまり問題文を「ある本を読んだところ50ページ残って、これが40%に相当する。この本は何ページあるか?」と読みかえることができます。すると、基本の式に当てはめると下のような式が成り立ちます。
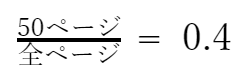
これを解いていきます。両辺に「全ページ」を掛け算して
- 50ページ = 0.4*全ページ
- 全ページ = 50ページ ÷ 0.4 = 125ページ
答え:125ページ
この方法は、問題文の解釈をちょっと変えるだけで計算過程を圧倒的に短くすることができるのでおすすめの方法です。
試験のときに、いきなり計算をし始めるのではなく、まずは問題文をじっくり読んで理解して「もっと簡単な言い換え、表現方法はないかな」と探す癖をつけましょう。
解説3
例題3
ある部活のメンバーが今年は20%増えて210人になった。昨年は何人だったか?
この問題も基本の式を使えば解くことがありますが、一つ注意しなければいけない点があります。それは「何を元の量(分母)にするか?」です。
問題文から、分母にするのは部活の(総)メンバーの人数だというのは分かると思いますが、ここで悩んでしまうのは、去年の部活の(総)メンバーか?今年のほうか?という点です。ここでは、問題文の読解力が必要になります。問題文には「部活のメンバーが今年は20%増えて」とありますがこれは「部活のメンバーが今年は(去年より、去年に比べて)20%増えて」ということを意味しています。
つまり、元の量(分母)は去年のメンバー、比べられる量(分子)は今年のメンバーとなります。これを踏まえて式をつくると下のようになります。
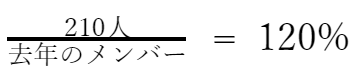
120%を分数で表すと120/100と表現できます。つまり
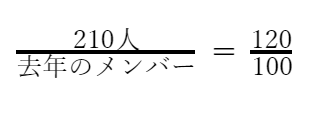
両辺に「去年のメンバー」と100を掛けます。
- 210人*100 = 120*去年のメンバー
次に、両辺を120で割ります。

答え:175人
NMAT割合 中級の例題_料金計算
例題 割引の問題
例題 割引の問題
ある遊園地では、大人の入園料は1500円、子供の入園料は大人の3割引きとなる。さらに10人以上で入園すると総額の1割引きとなる。大人10人、子供18人で入場したときの総額はいくらになるか?
問題文を見ると、何やら複雑な計算をしそうに思うかもしれませんが、焦ってはいけません。問題文の文脈通りに解いていきましょう。
まずは「大人の入園料は1500円、子供の入園料は大人の3割引きとなる」の部分です。このことから大人と子供の入園料を整理します。
- 大人:1500円
- 子供:1500円×(1-0.3)=1000円
次は「さらに10人以上で入園すると総額の1割引きとなる」とありますが、これは全員の入場金額を合計した後にその総額を1割引きにするので、一旦脇に置いておきます。
なので、次は「大人10人、子供18人で入場した」を計算します。
- 大人10人:1,500円 * 10人 = 15,000円
- 子供18人:1,000円 * 18人 = 18,000円
- 合計:15,000円 + 18,000円 = 33,000円
そして最後に脇に置いていた「さらに10人以上で入園すると総額の1割引きとなる」を計算します。
- 33,000円 * (1-0.1) = 29,700円
答え:29,700円
例題 複数の割引の問題
例題 複数の割引の問題
ある動物園の入園料は一人800円だが、団体割引があり、10人を超えた分は1割引きに、15人を超えた分は2割引きになる。この動物園に35人で入園したときの入園料は総額いくらになるか?
この問題も一見難しいように見えますが、1つ1つを整理すれば意外に簡単に解けます。まずは入園料について整理してみましょう。
問題文に「10人を超えた分は1割引きに、15人を超えた分は2割引き」とあります。これを整理すると
- 10人未満:1人あたり800円
- 10人を超えた分:1人あたり800円 * (1-0.1) = 720円
- 15人を超えた分:1人あたり800円 * (1-0.2) = 640円
次に、上の金額が適用される人数を確認します。
- 10人未満:「未満」は10人目を含まないので、9人
- 10人を超えた分:10人目~14人目の合計5人
- 15人を超えた分:15人目~35人目の合計21人
- 上の全ての合計人数:9+5+21=35人
「未満」「超えた分」などの表現は間違いをしやすいポイントです。上のように最後に合計人数を確認して、問題文と合うかを確認することをおすすめします。
それでは、上で整理した結果を足し合わせましょう。
- 800円*9人 + 720円*5人 + 640円*21人 = 7,200円 + 3,600円 + 13,440円 = 24,240円
答え:24,240円
NMAT割合 上級の例題_分割払い
例題
20,000円の自転車を購入し、購入時に総額の1/10を支払う。納品時に残りの2/5を支払う。この時残金はいくらになるか。
この問題で注意すべきポイントが2つあります。
- すぐに具体的な金額の計算をしない
- 「残りの2/5」に気をつける
1つ目は、問題文の冒頭に20,000円という具体的な数字があるので、すぐにこの数字を使いたくなってしまいますが、すぐにこの数字を使って計算すると、数字の桁数が大きくなり計算ミスの元になってしまいます。
2つ目は「残りの」というのがポイントです。これは、購入時に支払った総額の1/10を差し引いた金額からの割合になります。ここの意味を読み違えると不正解になってしまうので注意しましょう。
それでは計算していきましょう。
ポイント1つ目のとおり「20,000円の自転車を購入し」の20,000円という数字は一旦脇に置いておきましょう。
次は「購入時に総額の1/10を支払う」ですが、問題文は残金を求める問題なので、1/10支払ったあとの残金を計算します。
- 1 – 1/10 = 9/10
次は「納品時に残りの2/5を支払う」を計算します。上で計算した9/10の2/5なので、残金は以下のように計算します。
- 910*(1-25) = 910*35=2750
最後に購入金額から残金を計算します。
- 20000*2750=10,800円
答え:10,800円
NMAT・JMAT割合問題のまとめ
NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「割合問題」を解説します。
結論:割合問題でオススメの解き方
- 割合の問題は「比べられる量/元の量=割合」基本
- 複雑な問題文でも、文脈を1つ1つ整理する
- 割合の問題では、すぐに具体的な金額の計算をしない
- 「残りの」という表現に気をつける




