NMAT・JMAT時間切れ対策　無料問題集＆解説_確率問題

NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「確率問題」を解説します。

NMAT・JMATとは？

NMATは「管理者適正検査」と呼ばれ、中間管理職への昇進試験で使われる検査方法です。JMATは「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。

• 検査Ⅰ：言語能力適正検査(国語)　約30分
• 検査Ⅱ：非言語能力適正検査(数学)　約40分
• 検査Ⅲ：性格検査
• 検査Ⅳ：指向検査　Ⅲ,Ⅳ合わせて40分

この中でも「検査Ⅱ：非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。

「場合の数」の問題

例題
・３回連続でサイコロを降ったとき、１回目の数字＜2回目の数字＜３回目の数字となる組み合わせは何通りあるか？

解き方とコツ
・組み合わせ（樹形図）をすべて書きだそう

この問題のように「何通りあるか？」とたずねる問題は「場合の数」と呼ばれます。「場合の数」では、分数を使った確率で答えるのではなく、「〇〇通り」と整数で答えます。

そして「場合の数」の問題では「すべてのパターンを紙に書き出す」のが一番手っ取り早く、かつミスも少ない方法でおすすめです。

この例題では、１回目が一番小さい数字になり、2,3回目はそれよりも大きい数字で、2回目よりも3回目のほうが大きいので、1回目のサイコロの目でありえるのは

• １
• ２
• ３
• ４

の４パターンです。１回目に５以上の目が出てしまうと「１回目＜２回目＜３回目」が成り立たなくなってしまうからです。

まず、１回目が「１」だった場合を考えてみましょう。２回目のサイコロ目でありえるのは

• ２
• ３
• ４
• ５

の４パターンです。次に１回目の目が「１」、２回目の目が「２」のときの３回目のサイコロ目でありえるのは

• ３
• ４
• ５
• ６

の４パターンです。こんな感じで順番にすべてのパターンを書き出してみましょう。その結果が下のようになります。場合の数の問題を解くときには、必ず使う考え方なのでこの例題を使ってしっかり理解しておきましょう。

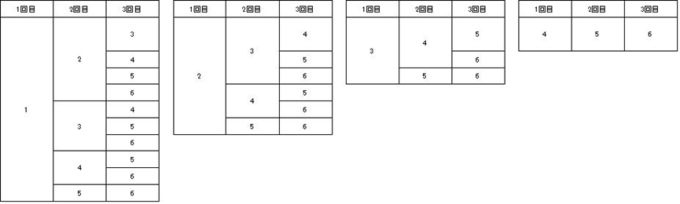
枝分かれのパターン数（＝３回目の目のパターン数）をカウントすれば、それが答えです。

答え：２０通り

「確率」の問題

例題
・２つのサイコロを同時に投げたとき、２つのサイコロの目の合計が９以上になる確率はいくらか？

解き方とコツ
・問題文のパターン数/すべてのパターン数で計算する

「確率」の問題が来たら、分母は全てのパターン、分子は問題文のパターンの分数で計算します。

まずは分母から考えてみましょう。全てのパターンとは、1回目のサイコロの目の全パターン数 × 2回目のサイコロの目の全パターン数 から求められます。つまり以下のようになります。

• 分母 = 6 × 6 = 36パターン

次に分子を考えます。2つのサイコロの目の合計が9になるパターンをすべて書き出してみましょう。すると、以下の４パターンであることが分かります。

• 1回目が３、2回目が６
• 1回目が４，2回目が５
• 1回目が５、2回目が４
• 1回目が６、2回目が３

「問題文のパターン数/すべてのパターン数」を計算すると

• 4/36 = 1/9

答え：1/9

「積の法則」の問題

例題
１：コインを4回連続で投げたとき、4回とも表になる確率はいくらか？
２：サイコロを3回投げるとき、1回目が１で、２回目と３回目が１以外になる確率はいくらか？

解き方とコツ
・１回ずつの確率を掛け算しよう

上の例題で、確率の問題は「問題文のパターン数/すべてのパターン数」で求めましょうというお話をしましたが、この問題のように、複数回の確率が重なり合うような場合（例：サイコロを３回投げる、くじを４回ひく等）では、１回ずつの確率を掛け算することで確率が求められます。

この問題のようにコインやサイコロを数回振る場合では、以下のように計算をしていきます。

• １回目の確率 × ２回目の確率 × ３回目の確率 × 4回目の確率 ・・・

コインは裏か表の2パターンしかありませんので、表が出る確率はずばり1/2になります。これが４回続くので、４回掛け算します。

• 1/2 × 1/2 × 1/2 × 1/2 = 1/16

答え：1/16

サイコロは６つの目があります。１が出る確率は1/6、１以外が出る確率は5/6です。つまり以下のように計算できます。

• 1/6 × 5/6 × 5/6 = 25/216

答え：25/216

「確率余事象」の問題

例題
・サイコロを２回連続で投げるとき、少なくとも１回は６が出る確率はいくらか？

解き方とコツ
・「少なくとも」は「１ー１回も〇〇しない確率」と読み替える

この問題では「少なくとも1回は・・・」の意味を理解することが最も重要です。

サイコロを2回連続で投げて「少なくとも1回は6が出る」とは具体的にどんな状況でしょうか？整理してみましょう。

• 1回目に6が出て、2回目に6が出ないパターン
• 1回目に6が出て、2回目も6が出るパターン
• 1回目に6は出ないで、2回目に6が出るパターン

の3パターンになります。

この3パターンを考え直してみると、実は次のように言い換えることができます。

• 全てのパターンから、1回目も2回目の6が出ないパターンを除いたパターン

ここまで理解できますでしょうか？そうしたらもう少し考えを進めます。「全てのパターン」とはつまり100％のことです。100％を分数で表すと1になります。そして、その1から「1回目も2回目の6が出ないパターン」を除いた残りを求めるので、以下の式が成り立ちます。

• 少なくとも1回は6が出る = １ – 1回も6が出ないパターン

それでは、これを使って計算していきましょう。「1回も6が出ないパターン」とは1回目も2回目も6以外の数字が出るパターンです。つまり以下のように計算できます。

• 1回も6が出ないパターン = 5/6 × 5/6 = 25/36

１からこの数字を引くと

• 1 – 25/36 = 36/36 – 25/36 = 11/36

答え：11/36

NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「確率問題」を解説します。