NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「集合応用問題」を解説します。
結論:集合応用問題でオススメの解き方
- 少なくとも→ベン図の2つの円を遠ざけよう
- 最大の→ベン図の2つの円を近づけよう
- 2×2→それぞれの集団に対してベン図を書いてみよう
- 3つの集合→3つの円のベン図を描こう
NMAT・JMATをもっと勉強したい↓
NMAT・JMATとは?
NMATは「管理者適正検査」と呼ばれ、中間管理職への昇進試験で使われる検査方法です。JMATは「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。
- 検査Ⅰ:言語能力適正検査(国語) 約30分
- 検査Ⅱ:非言語能力適正検査(数学) 約40分
- 検査Ⅲ:性格検査
- 検査Ⅳ:指向検査 Ⅲ,Ⅳ合わせて40分
この中でも「検査Ⅱ:非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。
「最大の」数を求める問題
例題
100人に電車と車について質問をしたところ、電車が好きと回答したのは65人、車が好きと回答したのが70人いた。このとき両方とも好きと回答した人数は最大で何人か?
「最大の」数を求めるポイント
ベン図の2つの円を近づけよう
集合の基本の問題の解説記事でも触れたとおり、集合の問題はベン図を使って解くことができる問題が多いです。ベン図についてわからない方は、こちらの記事の解説を御覧ください。
この問題も”ベン図を使って解くことができる問題”の一例です。
この例題でベン図を描くと、上のようになります。問題文で指示されている「両方とも好きと回答した人数」とは、上の絵の矢印の2つの円が重なり合う部分になります。
この部分を最大にするにはどうしたらよいか?
答えは「2つの円を近づける」です。
上のように、2つの円が近づくと、2つの円が重なり合う部分の面積が増えていきます。
そして、これが一番大きくなることを目的にどんどん近づけていきましょう。
すると、上のように大きい円の中に小さい円がすっぽり入ってしまいました。
これが、2つの円が重なる部分の大きさが最大になった、つまり問題で問われている答えになります。
このとき、2つの円が重なる部分の大きさ=小さい円の大きさになります。つまり、答えは小さい円の大きさ=電車が好きと回答した人数となります。
答え:65人
「少なくとも」の数を求める問題
例題
100人に電車と車について質問をしたところ、電車が好きと回答したのは65人、車が好きと回答したのが70人いた。このとき両方とも好きと回答した人数は少なくとも何人いるか?
「少なくとも」を求めるポイント
ベン図の2つの円を遠ざけよう
この問題でも、ベン図を使って考えています。
問題文で指示されている「両方とも好きと回答した人数」とは、上の絵の矢印の2つの円が重なり合う部分になります。
先程の問題は、この部分を最大にしましたが、今度は「少なくとも」なので最小にします。ではどうしたら、この部分は最小になるでしょうか?
その答えは「2つの円を遠ざける」です。
上のように、2つの円が遠ざかると、2つの円が重なり合う部分の面積が減っていきます。
そして、これが一番小さくなることを目的にどんどん遠ざけていきましょう。
すると、上のように円がベン図の壁にぶつかってしまいます。ここが2つの円を遠ざけることができる限界になります。
この壁=アンケートした合計人数になります。つまり、2つの円がベン図の壁にぶつかるとは「2つの円の合計面積=アンケートした合計人数」という式が成り立つと言うことになります。
- 2つの円の合計面積 = アンケートした合計人数
- 65人+70人−円が重なる部分 = 100人
- 円が重なる部分 = 65人+70人ー100人
- 円が重なる部分 = 35人
「円が重なる部分」とは「車も電車も好きと回答した人数」なので
答え:35人
2×2の集合問題
例題
男女100人ずつ、合計200人にうどんとそばの質問をした。質問の結果は以下のようになった。うどんもそばも好きな男性が15人、うどんだけが好きな女性が10人いたとしたとき、そばのみ好きな男女は何人いるか?
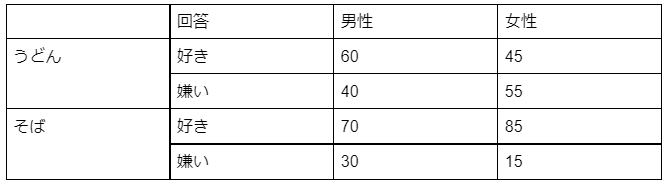
2×2の集合問題ポイント
それぞれの集団に対してベン図を書いてみよう
この問題では、男性と女性の2つの集団に対して同じアンケートがされています。問題文の表が複雑なので面食らってしまう人も多いかもしれませんが、慌てることはありません。
まずは男性の集団についてベン図を描いてみます。このとき、ベン図の円は、うどんとそばが”好きな”人数にします。理由は、求められる答えがそばだけが”好きな”人数なので、”好き”に合わせておいたほうが便利なためです。
2つの円の人数は表から読み取ります。問題文の「うどんもそばも好きな男性が15人」から、2つの円の重なる部分の人数も分かります。
すると、2つの円の重なり合う部分を除いた部分の人数もそれぞれ計算することができます。すると、求める答えのうち男性の人数を求めることができました。
- うどんのみ好きな男性 = 60人ー15人 = 45人
- そばのみ好きな男性 = 70人ー15人 = 55人
次に、女性の集団についてのベン図を描きます。
表と、問題文の「うどんだけが好きな女性が10人」から、上のようなベン図を描く事ができます。
このベン図から、2つの円が重なる部分=うどんもそばも好きな人の人数を求める事ができます。
- 2つの円が重なる部分 = 45人ー10人 = 35人
すると、そばだけ好きな女性の数も求めることができます。
- そばだけ好きな女性 = 85人ー35人 = 50人
それぞれの結果を足し合わせます。
- そばのみ好きな男女 = そばのみ好きな男性 + そばのみ好きな女性
- そばのみ好きな男女 = 55人 + 50人 =105人
答え:105人
3つの集合問題
例題
車・バイク・自転車を持っているかのアンケートを100人に行った。車を持っている人は15人、バイクを持っている人が20人いた時、次の問いに答えなさい。
- 車は持っているが、バイクを持っていない人は5人いた。このとき両方とも持っている人は何人いるか?
- 1.の情報に加えて、3つとも持っている人が3人、自転車を持っている人が10人いることが分かった。自転車を持っている人は車とバイクあるいはどちらも持っているとき、少なくとも2種類持っている人は何人いるか?
3つの集合問題のポイント
・3つの円のベン図を描こう
まずは1. について解説します。この問題では「自動車」と「バイク」しか登場しませんので、いままでと同様に2つの円のベン図を描きましょう。
上の図のようなベン図を描くことができます。すると、車を持つ15人から、車を持つがバイクを持たない5人を引いた、10人が両方とも持っている人数になります。
答え:10人
続いて、2. を解説します。この問題では「車」「バイク」「自転車」の3つが登場しますので、3つの円のベン図を描きます。
描かれたベン図は上の図のようになります。ここでポイントです。3つの円のベン図は複雑なので、3つの円それぞれの人数は円の外側に書くことをおすすめします。
そしてそれぞれの領域に当てはまる数を当てはめていきます。ここでポイントです。3つの円のベン図は複雑なので領域ごとに名前をつけましょう。
ここでは、アルファベットで上の図のように名前を振っていきます。
つぎに、このアルファベットを数字に言い換えられるかを考えます。問題文で「3つとも持っている人が3人」とありますので、dには3が当てはまります。
また1. の問題から、b+dが10だったことが判明しました。dが3なのでbは7になります。
問題文の「自転車を持っている人は車とバイクあるいはどちらも持っているとき」からgは0だということがわかります。
ここまでをベン図に書きこむと上の図のようになります。
ではここで、問題文をもう一度読み直してみましょう。求めるべきは「少なくとも2種類持っている人は何人いるか?」です。つまり、上のベン図で考えると、以下の合計数字を求めたいわけです。
- 7+3+℮+f
ここで、分からない℮とfが含まれる、自転車の円に注目しましょう。自転車の円を式にすると以下のようになります。
- 3+0+℮+f=10
- ℮+f=7
この結果を、上の式に代入します。
- 7+3+℮+f
- =7+3+7
- =17
答え:17人
まとめ
NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「集合応用問題」を解説します。
結論:集合応用問題でオススメの解き方
- 少なくとも→ベン図の2つの円を遠ざけよう
- 最大の→ベン図の2つの円を近づけよう
- 2×2→それぞれの集団に対してベン図を書いてみよう
- 3つの集合→3つの円のベン図を描こう





