NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「図表の読み取り」を解説します。
結論:図表の読み取りの解き方
- 表の縦と横の関係を理解する(誤解しない)
- 二段階表の構成を理解する
NMAT・JMATをもっと勉強したい↓
NMAT・JMATとは?
NMATは「管理者適正検査」と呼ばれ、中間管理職への昇進試験で使われる検査方法です。JMATは「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。
- 検査Ⅰ:言語能力適正検査(国語) 約30分
- 検査Ⅱ:非言語能力適正検査(数学) 約40分
- 検査Ⅲ:性格検査
- 検査Ⅳ:指向検査 Ⅲ,Ⅳ合わせて40分
この中でも「検査Ⅱ:非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。
基本の問題
例題
あるクラスで、好きな食べ物についてのアンケートをしたところ、下の表のような結果になった。このとき、A~Cに入る数値を答えろ。

ポイント
表の縦と横の関係を理解する。
表の問題のときは、まずは表の縦と横の関係を理解しましょう。
まず、縦の関係について考えてみましょう。一番上の行は食べ物の種類が書かれています。そして次の行が、それが好きだと回答した人の人数、そして最後の行が回答した人の割合です。
次に横の関係について考えてみましょう。左から2番目から5番目の列がアンケートへの回答結果です。一番右の列が、アンケートに回答した合計人数とその割合です。アンケートは50人に行われ、すべての人から回答を得られたので回答率は100%だということが分かります。
これを理解した上で、問題文を解いていきましょう。
まずはAです。Aが関連する横と縦の関係を注意深く観察しましょう。すると、横の関係から、以下の計算式が成り立つことが分かります。

- 15人+10人+20人+A=50人
- A=50人-15人-10人ー20人
- A=5人
これにより、表のAが埋まりました。

次にBについて考えてみましょう。Bが関連する横と縦の関係を注意深く観察しましょう。すると、縦と横の関係から、以下の計算式が成り立ちます。
- B=10/50
- B=0.2
- B=20%
これにより、表のBが埋まりました。

次にCについて考えてみましょう。Cが関連する横と縦の関係を注意深く観察しましょう。すると、横の関係から答えを求めることができます。

- 30%+20%+40%+C=100%
- C=100%-30%-20%-40%
- C=10%
別解)縦の関係から、以下の計算式で解いてもOKです。
- C=5/50
- C=0.1
- C=10%
答え: A=5人 B=20% C=10%
応用の問題(二段階表)
例題
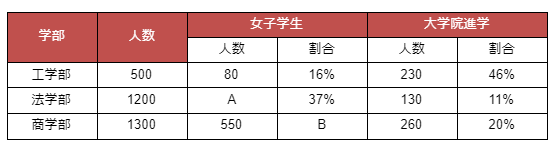
ある大学の4年生に対して、女子学生の割合と、大学院進学生の調査をした結果、以下の表のようになった。
- 問1.A、Bを埋めなさい。
- 問2.工学部の女子学生の進学率が30%のとき、工学部の男子学生の進学率は何%か?
ポイント
二段階表の構成を理解する
応用問題でも、表を良く理解することが重要です。この表の構成を理解しましょう。
左2つの列は、それぞれの学部と人数を表しています。そして真ん中の2列は、それぞれの学部の人数のうち女子学生の人数と割合を示しています。そして右の2列は、それぞれの学部の人数のうち大学院に進学する学生の人数を示しています。
ここで注意すべきは、「女子学生」と「大学院生」はそれぞれ独立しているという点です。つまり、女子学生の中には、就職する人も大学院に進学する人もいますし、大学院生の中には男子学生も女子学生も含まれた人数になっています。
問1
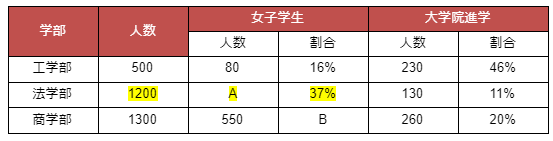
A、Bを埋めなさい。
問1は基本の問題と同じように、表の横と縦の関係から計算することが出来ます。
まずはAから解いていきましょう。Aの行に注目すると、以下の式が成り立ちます。
- A=1200×37%
- A=1200×0.37
- A=444人
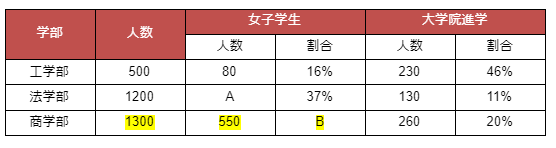
次はBです。Bの行に注目すると、以下の式が成り立ちます。
- B=550/1300
- B=0.42≒42%
答え:A=444人 B=42%
問2
工学部の女子学生の進学率が30%のとき、工学部の男子学生の進学率は何%か?
「工学部の男子学生の進学率」を求めるためには、以下の計算をする必要があります。
- 工学部の男子学生の進学率=進学する男子学生の数/工学部の男子学生の数
右辺の「進学する男子学生の数」と「工学部の男子学生の数」を計算しましょう。
まずは前者から。問題文の前半をヒントにします。「工学部の女子学生の進学率が30%」から「進学する女子学生の数」を計算します。
- 進学する女子学生の数=80人×30%
- 進学する女子学生の数=80人×0.3
- 進学する女子学生の数=24人
工学部で大学院に進学する人数は230人です。進学する女子学生の数が24人なので、以下の通り計算できます。
- 進学する男子学生の数=230-24=206人
次に後者です。
- 工学部の男子学生の数=500-80=420人
よって、以下の通り答えを求めます。
- 工学部の男子学生の進学率=進学する男子学生の数/工学部の男子学生の数
- 工学部の男子学生の進学率=206人/420人=0.49=49%
答え:49%
応用の問題(割合のみの問題)
例題
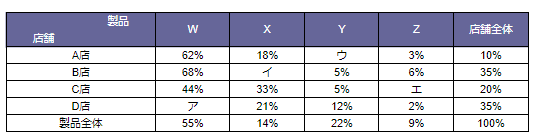
とある企業では、W,X,Y,Zの製品を販売している。下の表はA,B,C,D店におけるW,X,Y,Z商品の売り上げの割合を示したものである。一番右の数値は店舗ごとの売上金額が全店舗の売り上げに占める割合を表したものである。
- 問1 ウの数字を求めよ。
- 問2 全体に占めるB店のXの売り上げは何%か?
ポイント
横と縦の関係を誤解しない。
問1
ウを求めよ。
問題文に「 W,X,Y,Zの製品を販売している 」および「 A,B,C,D店におけるW,X,Y,Z商品の売り上げの割合を示したもの 」とあります。つまりウを求めるためには、A店での売り上げを見てみます。100%から他の製品の売り上げの割合を引けば良いのです。以下の式で求められます。
- 62%+18%+ウ+3%=100%
- ウ=100%-62%-18%-3%
- ウ=17%
答え:17%
問2
全体に占めるB店のXの売り上げは何%か?
ポイント
全体におけるB店の売り上げ × B店でのXの売り上げ を求めえる
全体におけるB店の売り上げは、一番右の列に書いてあるとおり35%です。
そして、B店におけるXの売り上げは問1と同じ方法で求めます。
- B店におけるXの売り上げ=100%-68%-5%-6%
- B店におけるXの売り上げ=21%
よって、以下の式で計算します。
- 35% × 21%
- =0.35×0.21
- =0.0735=7.35%
答え:7.35%
まとめ
NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「図表の読み取り」を解説します。
結論:図表の読み取りの解き方
- 表の縦と横の関係を理解する(誤解しない)
- 二段階表の構成を理解する




